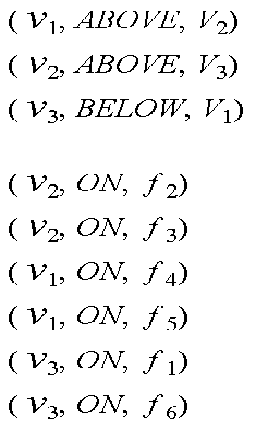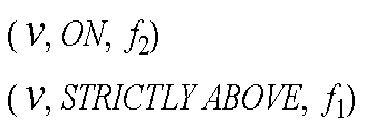"Geometry has not died because it is essential to many human activities
and because it is so deeply embodied in how human thinks.
With the introduction of computers with rich graphical capacities and the
recognition of multiple ways of learning, our current situation offers an
unprecedented opportunity for geometers and those work visually."

Walter Whiteley -The Decline and Rise of Geometry in 20th Century North America, 1999


 
 

Sugihara's Theorem

By now we have studied three necessary conditions for the realizability problem, all of them seem very nice but regretly not sufficient for solving this problem. Within the period 1982-1984 Sugihara finally proposed a complete set of constraints that characterizes realizable line drawings. These are derived as follows:

Step one: First, the labeling of the edges is used.
Step two:  Then, the spatial structure is derived from the edge labels:  a set of abstract triples expressing position relationships between vertices and faces. There are two types of triples:
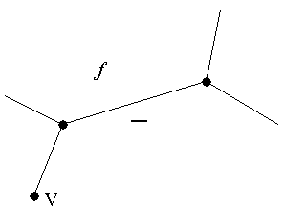
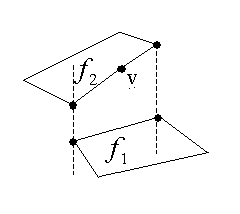
  1. Vertex-face triples of the form (v, r, f ), where v is a vertex of the drawing,  f is a face, and r is a relationship giving the position of  v relative to f . The possible values for r are"ON", "STRICTLY ABOVE", "STRICTLY BELOW", "ABOVE", and "BELOW",according to wherev must lie exactly on the face-plane  f , or strictly above/below f, or above/below  f  but possibly on  f  too, respectively.
  2. Vertex-vertex triples of the form(vi, r, vj), where vi and vj are vertices and r is a relationship giving the position of  vi relative to vj. The possible value for r are, "ABOVE", and "BELOW", depending on whether the z-coordinate of  vi is greater than that of  vj or conversely.


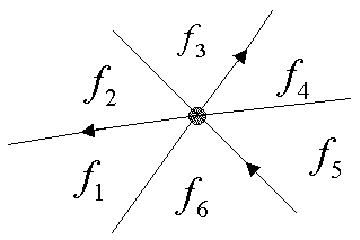
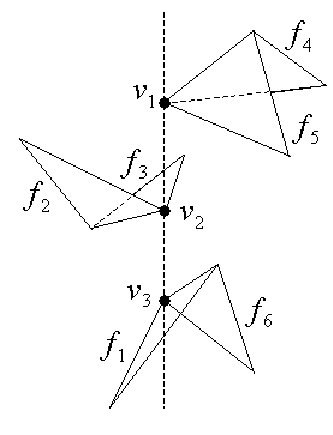
    3. According to the labels every vertex and edge produce a number of such triples, as shown in the following figure:

Feature
Spatially interpreted as
Triples added
( v, STRICTLY BELOW,  f  )

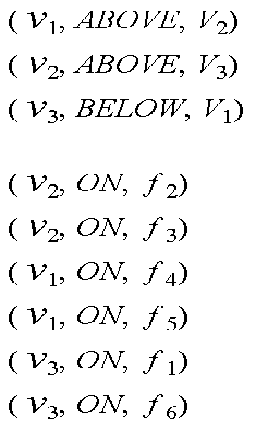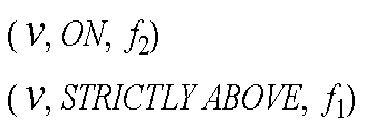            Figure:  The Spatial Structure.

 
Step three:  translate them into an algebraic constraint, as indicated in the following table:
Triple type
Relationship
Translated to constraint
vertex-face
    ( v ON f  )
   ( v ABOVE f  )
   ( v BELOW f  )
   ( v STRICTLY ABOVE f  )
   ( v STRICTLY BELOW f  )		 (vx, vy, vz, 1) * (Af , Bf , 1, Df )t  =  0
(vx, vy, vz, 1) * (Af , Bf , 1, Df )t  >=  0
(vx, vy, vz, 1) * (Af , Bf , 1, Df )t  =<  0
(vx, vy, vz, 1) * (Af , Bf , 1, Df )t  > 0
(vx, vy, vz, 1) * (Af , Bf , 1, Df )t  < 0
vertex-vertex
    (vi ABOVE vj)
   (vi BELOW vj)		     v1z - v2z >= 0
    v1z- v2z =< 0

Table:  Translation of incidence triples.


There, vx, vy and vz are the coordinates of vertex v, and Af , Bf  and Df are the plane coefficients of face f . These constraints are linear, since vx and vy are known and equal to the coordinates of the corresponding junction in the drawing. If we have n vertices and m faces, then there are 3m+n unknowns. We can collect them in a (3m+n)-tuple W, and write all equations in matrix form as:

A*W = 0             (1)
B*W > 0             (2)
where A and B are constant matrices made up of vertex coordinates. Sugihara proves the following:

Theorem: For a type-PAK problem with Assumptions O1, W2, D1 and D2, a polyhedron is realizable if and only if there is a solution of the linear system consisting of eq. (1) and ineq. (2).

We can see,  this is a Necessary and Sufficient Condition for the Realizability.
 

Problem with it

Sugihara's theorem gives a method for judgement of the realizability. However it is too strict from a practical point of view, slight perturbations of vertex positions can make a line drawing incorrect. In the realistic application, it is impossible to guarantee the exact position of objects in a scene. As we have mentioned before, in that Truncated Pyramid Question, figure (a) is generically reconstructible. So, some uncertainty must be taken into consideration. In order to correct super strict incorrect pictures, Sugihara proposes a nice solution: to delete from the equations those constraints that lead to this superstrictness by using the purely combinatorial concept of position-free incidence structures. People who are interested in this solution can find more details in the paper References (2).
 

A little bit more talk ...

I. Shimshoni and J. Ponce propose a variation of Sugihara's approach. They define a system similar to Sugihara's but, unlike Sugihara, they do not eliminate constraints that lead to a superstrict set of equations, but explicitly introduce uncertainty in these constraints. A necessary condition for a line drawing to be the correct projection of a polyhedron is that this system admits a solution, which again can be tested using linear programming.

As far as our problem is concerned, the work of several combinatorial geometers is often unnoticed by the robotics community. In this sense, H. Crapo and W. Whiteley have been investigating the connection between the realizability of linear scenes and the rigidity of planar bar frameworks. An interesting result they have proved is that a line drawing is consistent if and only if the planar bar framework it represents supports a non-null pattern of stresses on the bars. Hence, the realizability of a drawing and the rigidity of a framework have been proved to be connected problems.
 
 

Reciprocity ConditionHomeGoing to 3D-Space