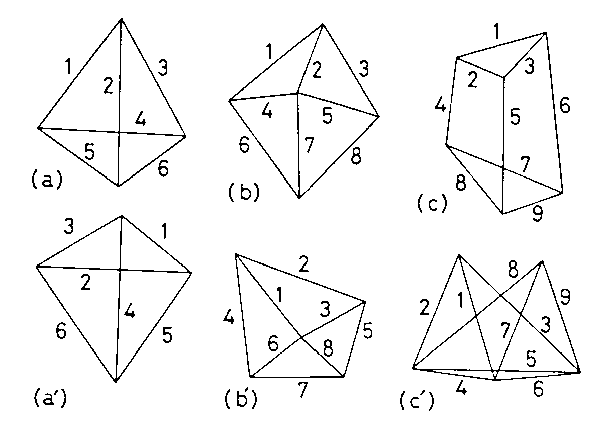
Figure: Reciprocal pairs of diagrams.
E. H. Gombridge --Art and Illusion, 1960.
If hidden edges are also drawn in the line drawing, the Perpendicularity Condition can be replaced with a stronger condition, the Reciprocity Condition. Firstly we explain what reciprocity means here. We define several notations.
Obviously, a line drawing is a diagram.V: the vertex set
E: the edge set
Rn: the n-dimensional Euclidean space
h: a mapping from V to Rn
G = (V, E): a graph consisting of S and E
Diagram: a triple D = (V, E, h)
Reciprocal
Let D = (V, E, h) and D' = (V', E', h') be two diagrams.
Reciprocal: D
and D' are said to be reciprocal if there is a one-to-one correspondence
between E and E', so that corresponding pairs of edges are perpendicular,
and corresponding edges converging to a vertex in one diagram form a close
path in the other.
Now let's see an example:

The above figure gives three pairs of diagrams that are reciprocal. In each pair the corresponding edges are labeled with the same number. We see, for example, that the six pairs of edges in (a) and (a') are mutually perpendicular, and that the three edges 1, 2, and 3 in (a) are converging to a vertex whereas the corresponding three edges in (a') form a closed path.
Reciprocity Condition
Now we add several more notations:
The vertex-edge diagram can be thought of as the picture of P in which hidden lines are also drawn by solid lines(that is, a picture in Assumption D3);P: a polyhedron
F: the face set
VG(P) = (V, E): vertex-edge graph of P
FG(P) = (F, E): face-edge graph of P
hv: a mapping from V to R2
hv(v): the orthographic projection of the vertex v onto the xy plane
hF: a mapping from F to R2
hF( f ): the gradient of the face f
VD(P) = (V, E, hv): vertex-edge diagram of P
FD(P) = (F, E, hF): face-edge diagram of P
A theorem has been proved by some people(Maxwell, Cremona, Whiteley and Sugihara).
Theorem: For any polyhedron P fixed in the space, the vertex-edge diagram and the face-edge diagram are reciprocal.
From this theorem, we obtain the Reciprocity Condition.
Reciprocity Condition: for a type-PK problem with Assumption D3 or D4(i.e. hidden lines are drawn in the line drawing), a polyhedron is realizable only when the line drawing has a reciprocal diagram.
In above figure, the pictures in (a), (b), and (c) are vertex-edge diagrams
of a tetrahedron, a quadrilateral pyramid, and a triangular prims. Indeed,
they have reciprocal diagrams as shown in (a'), (b'), and (c').
Discussion
However, the Reciprocity Condition is not sufficient,
either, for a picture to represent a polyhedron. The line drawing
in figure (c') has a reciprocal diagram as shown in (c), but obviously
it does not represent any polyhedron. So, the Reciprocity Condition is
only a necessary condition.