A projected truncated pyramid
Richard Feynman
Projective Conditions
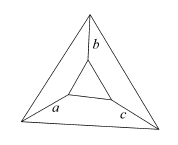
Usually, an arbitrary line-drawing is not correct. The positions of the vertices must accomplish certain projective conditions --incidence relations that would hold in a spatial interpretation, and hence must hold too in a projection. For example, the following drawing of a truncated pyramid is only correct when the three edges a, b and c, when extended, concur at a common point--the apex of the full pyramid, if it was completed.

A projected truncated pyramid
When this concurrence constraint is fulfilled, every pair of adjacent faces in the drawing can be lifted to a pair of non-coincident planes in 3D-Space, while keeping the coplanarity of cofacial vertices, and the contact along their common edge. On the contrary, when edges a, b and c do not concur at a common point, we cannot obtain such a spatial lifting. To see this, consider the drawing as lying on a plane in 3D-Space:
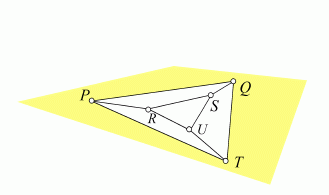
Here, we can fix the heights of P, Q and T say to lie on the drawing plane. Then, by giving a height to R over the plane, the height of S is completely determined by the coplanarity constraint on the face PQRS. Likewise, the height of U is determined by the coplanarity constraint on USQT, but... also by the coplanarity of U, R, P and T!. In general, both heights (say U' and U") do not necessarily coincide:
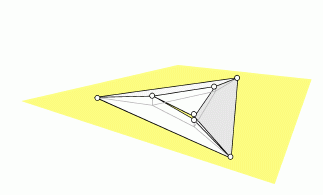
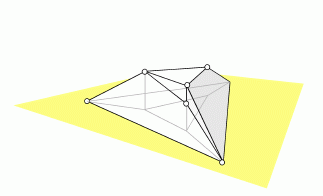
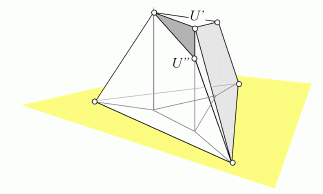
So, when a, b, c are not concurrent the only lifting that keeps adjacent
faces in the drawing also adjacent in 3D-Space is the trivial
one, with all points coplanar. When the projective condition of concurrence
holds we can obtain sharp liftings
with all pairs of adjacent faces lying on different planes in 3D-Space.
Lifting the drawing to 3D-Space
In fact, you can also think of the realizability problem as the
following equivalent problem formulation, which emphasizes the dependence
of the heights of some vertices with respect to others: Assume that the
drawing is described in terms of a set of vertices V and faces F. Each
face establishes a coplanarity constraint: if face f contains the vertices
P, Q, R, ... then it is required that in the spatial interpretation these
vertices are coplanar.
So the question is:
Is it possible to lift the vertices from the drawing plane to 3D-Space (along the imaginary rays of projection) in such a way that all coplanarity constraints are fulfilled and for each segment the corresponding faces in space are different?If the only possible lifting is the trivial flat one, with all vertices coplanar, then the drawing is incorrect. The drawing is correct if there is a sharp lifting, one where every two adjacent faces lie on different planes in 3D-Space.
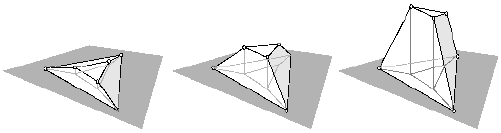
Spatial liftings of a correct truncated pyramid
Classification of drawings
Line drawings can be classified into four classes, according to their
combinatorial structure.
 |
Always correct
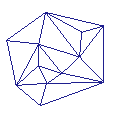
Some drawings are always correct regardless of the geometric positions of their junctions on the plane. For example, line drawings where all faces are triangles fall into this category: they can be "lifted" to 3D-Space by giving arbitrary heights to the vertices. Since three points are always coplanar, coplanarity constraints will trivially hold at all faces, regardless of the chosen heights. (In the example to the left, assume that the vertices of the external contour need not be coplanar.) |
 |
Always incorrect
On the other hand, there are drawings that are always incorrect independently of the positions of the junctions.example in this class is Penrose's tribar, an "impossible figure". |
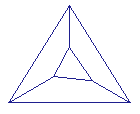 |
Almost always
incorrect
These drawings are only correct when the junctions are at special positions satisfying certain projective conditions, conditions that hold in 3D-Space and are projectively invariant. For example, this truncated pyramid is only correct when the three edges joining the two triangles concur to a common point. |
 |
Almost always
correct
In them, when the junctions are in a generic position the drawing is correct. However, at special positions, you could find a pair of faces that lift to the same plane in 3D-Space (meaning that they actually do not produce a boundary segment between as indicated in the drawing). |