Walter Whitely --The Decline and Rise of Geometry
in 20th Century North America, 1999 [125].
A perpendicularity property
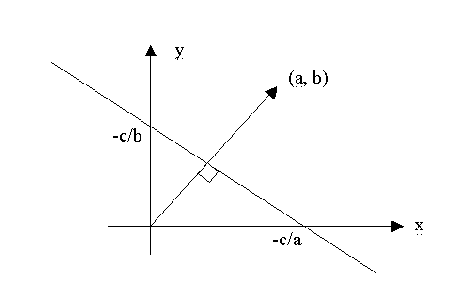
Besides the Labeling algorithm, there is still another very elegant theorem used for the recognition of the line drawings, which is called the Perpendicularity Condition. This theorem is based on the following remarkable property: in the 2D-space, i.e. xy plane, an arbitrary line can be represented by equation ax+by+c = 0, this line is perpendicular to the vector (a, b), as showed in the following figure:

Perpendicularity in the Gradient Space
With this remarkable geometric property, we can conclude the Perpendicularity Condition. Firstly we need definitions of several new concepts. Let P be a polyhedron fixed in the space, and fj be the jth face of P. Let equation
Let f1 and f2 be two faces that share a common edge. The orthographic projection of this edge onto the xy plane is represented by the equation:Gradient: the order pair Gj = (aj, bj) is called the gradient of the surface.
Gradient Space: a 2D space with the (a, b) coordinate system. Obviously, Gj is a point in this gradient space.
Perpendicularity Condition
We can use the above perpendicularity property to check the realizability problem, that is:
Theorem: For a type-PK problem, a polyhedron is realizable only when the faces can be mapped to distinct points in the picture plane in such a way that, if a pair of faces share a common edge, the line connecting the corresponding pair of points is perpendicular to the image of the edge.
Now we can use this theorem to check that tricky Truncated Pyramid Question. As shown in the (a) of the following figure:
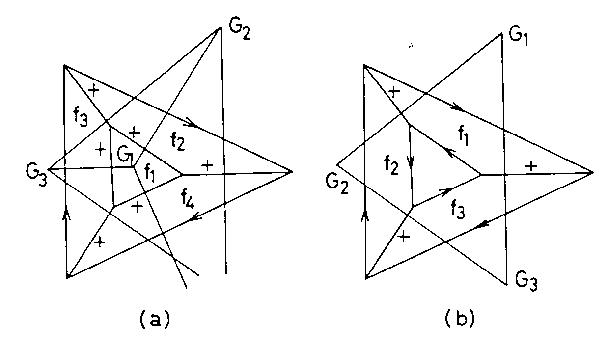
Figure: Perpendicularity Condition.
We can plot the first point G1 arbitrarily and the second
point G2 in an arbitrary distance from G1. If we
proceed plotting G1, G2, G3 in this order
using the Perpendicularity Condition stated
in the Theorem, we find that the last point G4 cannot be plotted.
Thus, we can recognize the inconsistency in interpreting the picture as
a truncated pyramid.
Discussion
However, this condition is not sufficient.
For example, a labeled line drawing in the (b) of the above figure represents
the interpretation of the picture as an object that is obtained from a
truncated pyramid by digging a hole so that a triangular top face is replaced
with a hole penetrating the object. This interpretation is likewise incorrect,
but we can plot the gradients of all the three visible faces without violating
the Perpendicularity Condition, as shown in
(b). Thus, this condition is necessary but not sufficient even if there
is no overlap among visible faces.
Well, let's move on toward our aim ! In the following part, we are
going to introduce another interesting condition which is called the Reciprocity
Condition.