James Burke ---The Pinball Effect. How Renaissance
Water Gardens Made The Carburetor Possible, 1996 [14].
In the progress of line drawing interpretation, a very interesting algorithm
was developed by Huffman, which is called
Labeling
Scheme. This algorithm is used to solve the type-PA problems with
assumptions O1, O4, W3, D1, and D2, that is, a realizability problem of
a hidden-line-eliminated line drawing in the trihedral object world with
the nonaccidentalness assumption. So we know that each line in the picture
corresponds to exactly one edge of the object. The algorithm classifies
the lines into three categories and assigns different labels to them.
First, we define two types of edges:

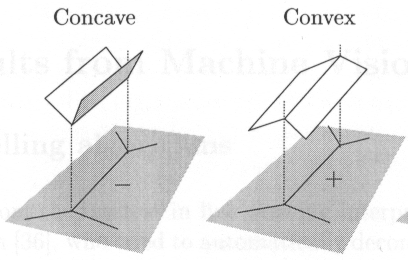
The meaning of concave and convex are quite obviously here, an edge is convex(concave) if it can be spatially interpreted as a convex(concave) edge between two spatial faces. Then we classify each edge into one of the following three categories.
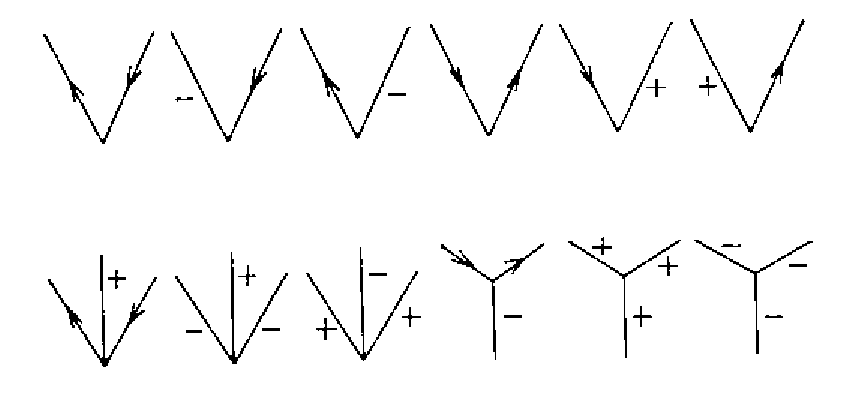
Figure: List of possible vertices in the trihedral object world
All other labelings are impossible. With this labeling scheme, we can quickly find that in the following figure:
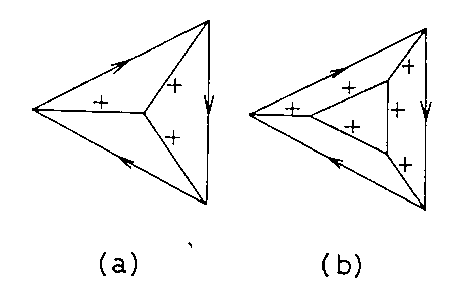
The labeling in (a) corresponds to the interpretation of the picture as a triangular pyramid, and that in (b) as a truncated pyramid. This algorithm is quite simple and the number of possible cases is also rather small, only twelve. All the line drawings of those possible polyhedrons under those assumptions (O1, O4, W3, D1, and D2) must correspond to one of the twelve labelings. How well it would be if any one of the twelve labelings also must corresponds to a correct polyhedron ! However, regretly the answer is NO. We can easily find an picture which has a consistent way of labeling, but it does not correspond to any polyhedron. For example:
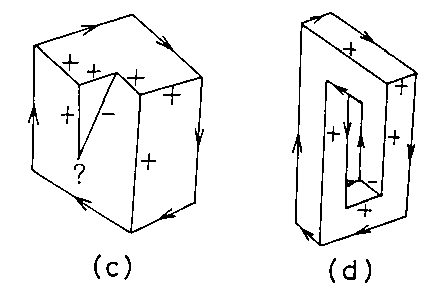
Thus, for a picture to admit a consistent labeling
is only a necessary, but not sufficient, condition for the picture to represent
a polyhedron correctly. A labeling that is consistent with those
twelve cases gives merely a candidate for the spatial structure of the
object. Let's go forward toward our goal ......